Thank you for the more detailed exposition of etendue conservation. I still don’t believe that my formula violates it at all, but have come to realize that there are 2 potential misunderstandings in our discussion:
- The formula being proposed is for the angle of the hotspot, not the entire beam, and not even all of the light that hits the reflector–some of that ends up as corona. So applying conservation of etendue for the light that hits the reflector, i.e., hotspot + corona, does not disprove a formula for the hotspot alone.
- It is conceivable that we are working with different definitions of the same term. To be more precise than before, I will try to give rigorous definitions, plus examples, for the following terms. You may feel free to disagree with my definitions, as long as you provide yours.
- Hotspot: region in space where, for an observer located there, the entire rim of the reflector is visible and lit by reflection of the LED.
- Corona: region in space where there exists some point of the reflector that is visible and lit.
- Spill: region in space where there exists some point on the LED that is directly visible.
By the above definitions, the hotspot is always a subset of the spill: if you can see the entire rim of the reflector at all, you are within the tangent cone of that rim, which always contains the emitter. Trivially, the hotspot is also always a subset of the corona. It does not necessarily always hold that the corona is a subset of the spill: sometimes the spill can be narrower.
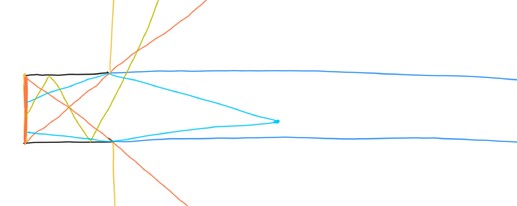
To give a simple and illustrative example, consider a cylindrical reflector, with the emitter consisting of the entire base of the cylinder.
Orange vertical segment is emitter, black is reflector.
- The hotspot is the infinite solid cylinder enclosed by the blue lines. A cyan-colored “witness point” is shown to be inside the hotspot, via the two light paths from the reflector’s rim. In this setup, the hotspot has zero divergence angle, and in the limit (for a far enough observer), consists of 0% of the emission.
- The spill is the cone enclosed by the orange rays: in this cone, you can always see some part of the emitter directly.
- The corona is the entire half-plane to the right of the reflector’s opening. There’s a dark yellow-green ray in this region that gets reflected twice before exiting; nevertheless, the observer far out in the ray would see the ray’s last point of incidence on the reflector as lit. Note that in this case, the corona is wider than the spill.
That said, I do not claim that my original formula works for extreme setups like this: estimates such as small-angle approximations (which stem from the assumption of a small emitter) were used freely without a quantitative error bound.