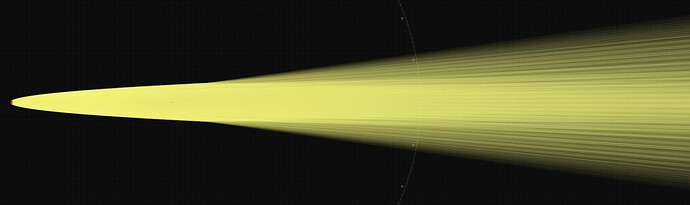
Sure! My first attempt defines the hotspot as “a region that captures all of the light hitting the reflector and has a constant intensity equal to the maximum intensity of the light”. Of course, this is a very crude definition and does not account for the presence of the corona, or the fact that the hostpot is not quite constant in intensity.
My derivation in this topic defines the hotspot as the region where the entire rim of the reflector appears to be lit. From my observation of various flashlights (walking to the target and looking into the reflector), this definition captures exactly what part of the beam I would classify as hotspot.
I would argue that the non-monotonicity is indication that the formula is doing something right!
For a perfectly Lambertian source, and ignoring truncation at the base of the reflector, the intensity of the beam depends on the reflector only via the diameter, not on height. Thus, as long as the diameter is fixed, the maximum intensity achieved stays the same.
Now consider what happens to a reflector if you fix the diameter and let height range from 0 to infinity. At height 0, the portion of light captured (p) equals 0. At height infinity, p = 1. Thus, p can be thought of as a “rescaled” version of reflector height.
Now, fixing constant the diameter (and thus intensity, and thus cd/lm, and thus acuity), consider what happens to hotspot angle as height increase from 0 to infinity:
- At height close to 0, the reflector captures only a tiny amount of light, but still must achieve the maximal hotspot intensity. Thus, the hotspot must be small.
- At height close to infinity, the reflector captures almost all of the light, but the spill angle becomes very narrow due to the elongation. Since the hotspot cannot be wider than the spill, the hotspot is also forced to be very small.
At this point, we have established that:
- At height close to 0 (thus p close to 0), the hotspot angle approaches 0.
- At height close to infinity (thus p close to 1), the hotspot angle approaches 0.
So however the constant in front of 1/Acuity depends on p, the dependence f(p) must satisfy f(0) = 0 and f(1) = 0. If the claim f(p) = sqrt(p(1-p)) has any chance of being correct, it must satisfy the above boundary conditions.
The problem of generalizing these calculations to other optical systems is interesting. For LEPs, it’s unclear whether the emitter can be modeled by a Lambertian at all. For convex lenses like Z1, the roles of hotspot and spill are exchanged, and there is no corona. I’m happy to do the analogous calculations later today, which I expect to be way simpler than for a reflector.
I would argue that the resemblance among the different models is an essential feature of the physical system we try to model, and in no way a miracle or coincidence!
I agree that the full/diametrical divergence angle is most useful for most folks. They may also prefer using degrees over radians, which is a bit unfortunate: radians are the natural units to work with mathematically, but degrees normalize commonly encountered angles into the natural interval [1,10].
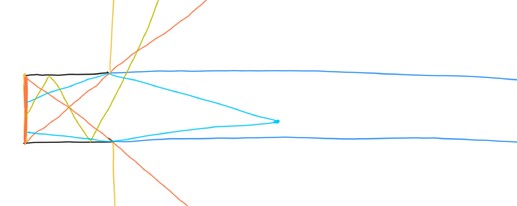
On a tangential note: I think my ray-tracing method can give you an explicit formula (though not necessarily closed-form) for the entire angular distribution of the beam. The computation may be long, but I’ll do it if you’re interested! Once I do it, I hope that it correctly predicts the separation of the beam into hotspot, corona, and spill.